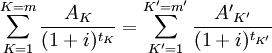We are using BigDecimal in many places. We are using BigDecimal for modeling currencies, financial measures (interest rates, coefficients), maybe some other domain values that needs precision better than Double provides.
BigDecimal is common and straightforward answer for precision problem, but why it sucks?
First problem with BigDecimal is lack of power function - there is no BigDecimal^BigDecimal. Of course this is not a real problem - you can use some external library for doing this or write this one on your own. To do this we have to implement e^x ln(x) and n! - piece of cake. Frustration is bigger if you try to find a lib for that.
Second problem is that even you solve the first problem there is new - performance problem. This problem accompanies us as a humanity for ages. If we want to perform operations with precision better than float or double offers we have to struggle with numerical recipes and lack of low level support. This one is quite interesting.
What is my understanding of low level support? Lets go back in time to 286 (Intel 286 not A.D. 286). There were no low level support for floating point operations at all. For 386SX there were new option to buy 387 floating point co-processor to perform floating point operations faster. There were also software emulators for 387 (to run apps written for 386DX with embedded 387 on plain 386SX). From that time later on Intel integrate those two chips in one. Modern IA-64 processors delivers floating point programming model based on separate instruction set to perform operations like add and multiply. As we know from math perspective it is enough to implement more sophisticated functions like e^x, ln x and others. We have also support to approximate reciprocal for floating point number and therefore we can divide by float because division is just a multiplication by reciprocal. Those operations are faster than those you can implement in plain assembly. But can we benefit from this mechanism in BigDecimal computations?
To answer this question we have to go deep to the assembly language. For java this is surprisingly quite easy. If we add "-XX:+UnlockDiagnosticVMOptions -XX:+PrintAssembly" to java command line and make it work. We will get assembly for parts that was compiled with JIT. You should get something like this:
Decoding compiled method 0x000000010fdffd90:
Code:
[Entry Point]
[Constants]
# {method} {0x0000000123bb5310} 'multiply' '(Ljava/math/BigDecimal;)Ljava/math/BigDecimal;' in 'java/math/BigDecimal'
# this: rsi:rsi = 'java/math/BigDecimal'
# parm0: rdx:rdx = 'java/math/BigDecimal'
# [sp+0xf0] (sp of caller)
0x000000010fdfffe0: mov 0x8(%rsi),%r10d
0x000000010fdfffe4: shl $0x3,%r10
0x000000010fdfffe8: cmp %rax,%r10
0x000000010fdfffeb: jne 0x000000010fa45e20 ; {runtime_call}
0x000000010fdffff1: data32 data32 nopw 0x0(%rax,%rax,1)
0x000000010fdffffc: data32 data32 xchg %ax,%ax
(...)
Code for "simple" multiplication fills few screens and takes a lot of compare and jump loops.
Long trace of this output is not interesting to follow, but there is no signs for floating point operations. It looks like our JIT don't find floating point operations useful for BigDecimal operations.
My personal experience with this effect was when I was implementing "better" way of computing APR. I have to implement a^x and therefore I was forced to implement e^x and ln x on my own. Of course it was based on multiplication/division and add operations. At the end - results was worse than I expected. For very common arguments for APR computations took more than second on my i5 CPU. During those computations one core was working on 100%. I won't merge this branch because it renders my library useless - I can't waste so much CPU time for computations of APR.
Third problem with BigDecimal is inconsistency of basic math operations like comparison value to another one. Lets focus on ZERO. This number is very important because we can't find reciprocal of ZERO. As a senior math user I was aware that division(x) will fail for x = ZERO and therefore I was checking if(x.equals(ZERO)) to prevent division. Unfortunately there is a case when x is not equal ZERO (x="OE-21") in terms of equals method, but it ends with "BigInteger divide by zero". Fortunately there is compareTo method which returns: -1, 0, or 1 as this BigDecimal is numerically * less than, equal to, or greater than val. To solve this issue you should compareTo val rather than check if it is equal to val.
Even though some problems of BigDecimal really annoys me I found it very useful for modeling math and financial domains. It has its own problems, but I will not implement this kind of functionality better on my own.